ТРЕУГОЛЬНИК СЕРПИНСКОГО
Фракталы вокруг нас повсюду, и в очертаниях гор, и в извилистой линии морского берега. Некоторые из фракталов непрерывно меняются, подобно движущимся облакам или мерцающему пламени, в то время как другие, подобно деревьям или нашим сосудистым системам, сохраняют структуру, приобретенную в процессе эволюции.
Х. О. Пайген и П. Х. Рихтер.
Треугольник Серпинского (Sierpiński triangle)
— фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского.



ТРЕУГОЛЬНИК СЕРПИНСКОГО
ПОСТРОЕНИЯ
Удаление треугольников
Треугольник Серпинского может быть построен из равностороннего треугольника путем повторного удаления треугольных подмножеств:
Начните с равностороннего треугольника.
Разделите его на четыре равносторонних треугольника меньшего размера и удалите центральный треугольник.
Повторяйте шаг 2 до бесконечности с каждым из оставшихся меньших треугольников.
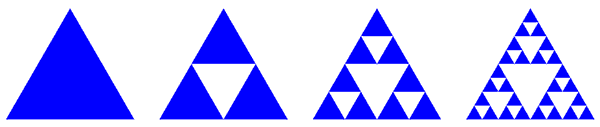
Каждый удаленный треугольник (трема) это топологически открытый набор . Этот процесс рекурсивного удаления треугольников является примером правила конечного подразделения
Та же самая последовательность фигур, сходящаяся к треугольнику Серпинского, может быть сгенерирована с помощью следующих шагов:
-
Начните с любого треугольника на плоскости (подойдет любая замкнутая ограниченная область на плоскости). В каноническом треугольнике Серпинского используется равносторонний треугольник с основанием, параллельным горизонтальной оси (первое изображение).1.
-
Уменьшите треугольник до 1/2 высоты и 1/2 ширины, сделайте три копии , и расположите три сжатых треугольника так, чтобы каждый треугольник касался двух других треугольников в углу.
Сжатие и дублирование

Можно обратить внимание на появление центрального отверстия, потому что три усохших треугольника между ними могут покрывать только 3/4 площади оригинала.
3 Повторите шаг 2 с каждым из меньших треугольников Этот бесконечный процесс не зависит от начальной формы. треугольник - так просто яснее. Первые несколько шагов, начинающиеся, например, с квадрата, также имеют тенденцию к треугольнику Серпинского.
Майкл Барнсли использовал изображение рыбы, чтобы проиллюстрировать это в своей статье «Фракталы с V-переменной и суперфракталы».
Игра хаос
-
Возьмите три точки в плоскости, чтобы сформировать треугольник, вам не нужно его рисовать.
-
Произвольно выберите любую точку внутри треугольника и примите ее текущее положение.
-
Случайно выберите любую из трех вершинных точек.
-
Переместитесь на половину расстояния от вашей текущей позиции до выбранной вершины.
-
Постройте текущую позицию.
-
Повторите, начиная с шага 3.
Этот метод также называется игра в хаос , и является примером системы повторяющихся функций .
Вы можете начать с любой точки вне или внутри треугольника, и в конечном итоге сформируется прокладка Серпинского с несколькими оставшимися точками (если исходная точка находится на контуре треугольника, оставшихся точек не будет). С помощью карандаша и бумаги краткий контур формируется после расстановки примерно ста точек, а детали начинают проявляться через несколько сотен.

Он формируется путем многократного изменения более простых кривых, аналогичного построению снежинки Коха :
-
Начать с одного отрезка на плоскости
-
Повторно заменять каждый отрезок кривой с тремя более короткими сегментами, образующими углы 120 ° на каждом стыке между двумя последовательными сегментами, причем первый и последний сегменты кривой либо параллельны исходному отрезку линии, либо образуют с ним угол 60 °.
Наконечник стрелы Серпинского
На каждой итерации это конструкция дает непрерывную кривую. В пределе они приближаются к кривой, которая очерчивает треугольник Серпенского одним непрерывным направленным (бесконечно изгибающимся) путем, который называется наконечником стрелки Серпинского .

Клеточные автоматы
Треугольник Серпинского также появляется в некоторых клеточных автоматах (таких как Правило 90 ), включая те, которые относятся к Игре жизни Конвея . Например, Жизнеподобный клеточный автомат B1 / S12 при применении к отдельной ячейке сгенерирует четыре приближения треугольника Серпинского. Очень длинная линия толщиной в одну ячейку в стандартной жизни создаст два зеркальных треугольника Серпинского.
Пространственно-временная диаграмма паттерна репликатора в клеточном автомате также часто напоминает треугольник Серпинского, такой как обычный репликатор в HighLife. Треугольник Серпинского также можно найти в автомате Улама-Уорбертона и в автомате Хекса-Улама-Уорбертона

Обобщение треугольника Серпинского также можно сгенерировать с помощью треугольника Паскаля , если используется другой модуль Modulo. Итерацию n можно создать, взяв треугольник Паскаля с P строками и раскрасив числа по их значению для x mod P. Когда n приближается к бесконечности, создается фрактал.
Тот же самый фрактал может быть получен путем разделения треугольника на мозаику из P похожих треугольников и удаления треугольников, перевернутых вверх ногами из оригинала, а затем повторения этого шага с каждым меньшим треугольником.
И наоборот, фрактал также можно сгенерировать, начав с треугольника, продублируя его и расположив n (n + 1) / 2 новых фигур в той же ориентации в более крупный аналогичный треугольник с вершинами предыдущие рисунки касаются, затем повторяют этот шаг.
Обобщение на другие модули
ИЗ ИСТОРИИ
Вацлав Серпинский описал треугольник Серпинского в 1915 году. Однако подобные узоры появляются уже в 13 веке Косматимозаики в соборе Ананьи , Италия и других местах центральной Италии, для ковров во многих местах, таких как неф римской базилики Санта-Мария-ин-Космедин , а также для отдельных треугольников, расположенных по кругу в нескольких церквях и базиликах. В случае изолированного треугольника итерация не менее трех уровней.
Средневековый треугольник с исторически достоверной датировкой был недавно изучен. Он сделан из порфира и золотого листа, изолирован, итерация 4 уровня
Аполлоническая прокладка была впервые описана Аполлонием Пергским (3 век до н.э.) и далее проанализирована Готфрид Лейбниц (17 век), и является искривленным предшественником треугольника Серпинского 20 века









