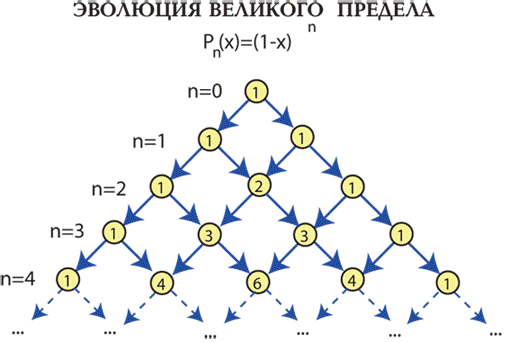
Треугольник Паскаля
Треугольником Паскаля называется бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке
Треугольник Паскаля и числа Фибоначчи
Если строки в треугольнике Паскаля выровнять по левому краю, то суммы чисел, расположенных вдоль диагоналей, идущих слева направо и снизу вверх, равны числам Фибоначчи — 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,…11235813213455891442333776109871597… (каждое число в этой последовательности равно сумме двух предыдущих, а начинают последовательность две единицы)
I'm a paragraph. Click here to add your own text and edit me. It’s easy.
Если раскрасить нечётные числа в треугольнике Паскаля в один цвет, а чётные — в другой, получится такая картина (указанным образом раскрашены числа в первых 128 строчках)
Треугольная таблица Пингалы
150 лет до нашей эры
Пингала — древнеиндийский математик, известный своим трудом под названием «Чандас-шастра» или «Чандас-сутра»
Разложение натуральных степеней бинома Пингалы
Лестница на гору Меру
Источник: Развитие комбинаторных сведений до середины 17 столетия (А Е Малых, А С Бойко Вестник Пермского Университета 2013 год)
СВОЙСТВА ТРЕУГОЛЬНИКА ПАСКАЛЯ
СВОЙСТВО 1
Треугольник Паскаля бесконечен
СВОЙСТВО 2
Сумма чисел в строках треугольника Паскаля = 2^n, где n - номер строки.
СВОЙСТВО 3
Треугольник Паскаля симметричен относительно центрального столбца
СВОЙСТВО 4
Первая диагональ треугольника Паскаля - это натуральные числа, расположенные по порядку
СВОЙСТВО 5
Вторая диагональ треугольника Паскаля - это «треугольные» числа. Можно заметить, что если к 1 прибавить 2, мы получим 3, если к 3 прибавить 3, мы получим 6, а если к 6 прибавить 4 по лучится10, и таким образом каждый может продлить этот бесконечный ряд самостоятельно
СВОЙСТВО 6
Третья диагональ треугольника Паскаля - это «пирамидальные» числа или, более точно, тетраэдральные числа, показывающие сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра)
СВОЙСТВО 7
Четвёртая диагональ треугольника Паскаля - это уже фигурные числа в четырехмерном измерении, поэтому это можно только представить в виртуальном мире
СВОЙСТВО 8
Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются)
СВОЙСТВО 9
Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредств енно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы)
СВОЙСТВО 10
В каждой строке треугольника Паскаля сумма чисел на нечётных местах равна сумме чисел на чётных местах
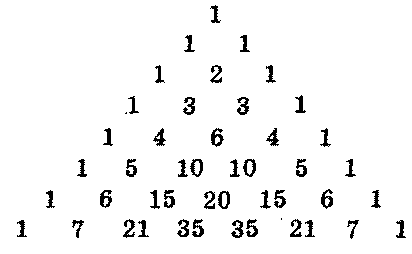
1+15+15+1 = 6+20+6
СВОЙСТВО 11
Если номер строки треугольника Паскаля – простое число, то все числа этой строки, кроме 1, делятся на это число
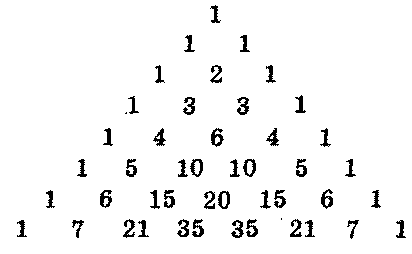
СВОЙСТВО 12
Если нечётное число в треугольнике Паскаля заменить на точки чёрного цвета, а чётные- белого цвета, то треугольник Паскаля разобьётся на более мелкие треугольники
СВОЙСТВО 13
Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А
О ТРЕУГОЛЬНИКЕ ПАСКАЛЯ
Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами (в математике биномиальные коэффициенты – это коэффициенты в разложении бинома Ньютона (1+х)n по степеням x. Коэффициент при xk обозначается ({\displaystyle \textstyle {\binom {n}{k}}}n/k) или{\displaystyle \textstyle C_{n}^{k}} Cn/k и читается «биномиальный коэффициент из n по k»), записанными в таблицу, которая выглядит как равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел, из-за этого треугольник можно продолжать до бесконечности.
Назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года - даты выхода "Трактата об арифметическом треугольнике". Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.